Het manipuleren van ongrijpbare golven zoals licht, geluid of elektronen, in periodieke structuren of kristallen, heeft iets mysterieus. In het toonaangevende natuurkundige wetenschappelijke tijdschrift Physical Review Letters, gepubliceerd door de American Physical Society, beschrijft een team van onderzoekers van de Universiteit Twente hoe elke soort kristal elke soort golf opsluit. De techniek werkt voor zowel quantum als klassieke golven. De resultaten geven met name een impuls aan efficiënte nieuwe geïntegreerde circuits die in minuscule lichtpulsen gecodeerde informatie door slimme steden sturen.
Golven vormen een onlosmakelijk onderdeel van ons dagelijks leven, of we nu naar muziek luisteren, onze reflectie in een spiegel waarnemen of een schip op de oceaan zien dobberen. Om ze te manipuleren moet je golven in een kleine oppervlak op kunnen sluiten. Wetenschappers weten al dat dit mogelijk is door opzettelijk afwijkingen van de perfecte periodiciteit in het kristal aan te brengen. Maar hoe worden de golven precies opgesloten? Worden ze in alle dimensies tegelijk opgesloten, of behouden ze de vrijheid om langs een lijn of in een vlak te bewegen? Opmerkelijk genoeg was de belangrijkste stap van het hebben van de structuur van het kristal naar het voorspellen van de opsluiting van de golven tot nu toe niet gezet.
Kristallen ontwerpen
Wellicht ken je kristallen die mineralen in de natuur vormen. Dergelijke kristallen kunnen worden gebruikt om quantummechanische elektronische golven op te sluiten. Door de mens gemaakte kristallen van silicium hebben geleid tot de ontdekking van elektronische transistoren, de basis voor de huidige digitale revolutie. We weten nu dat er andere soorten kristallen zijn, die in staat zijn om verschillende soorten golven zoals licht, geluid en mogelijk zelfs aardbevingen op te sluiten en te manipuleren.
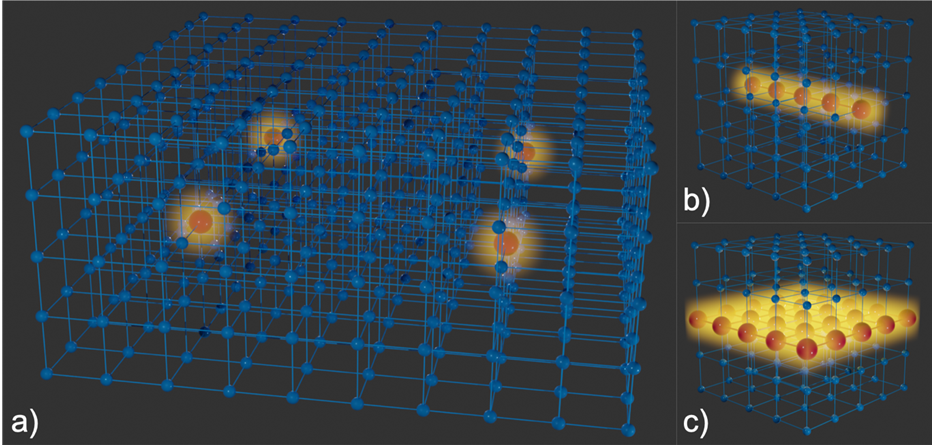
Figuur 1: Illustratie van een 3-dimensionaal kristal met verschillende soorten beperkende centra. Blauwe bollen stellen ongemodificeerde eenheidscellen voor, en rode bollen zijn opsluitende centra. (a) Kristal met vier beperkende centra, die elk tegelijkertijd golven (geel) in de drie dimensies (c=3) opvangen. (b) Kristal met een lineair beperkend centrum waar golven zich in 1 dimensie kunnen voortplanten, analoog aan een optische vezel (c=2). (c) Kristal met een plenair beperkend centrum waar golven zich in 2 dimensies kunnen voortplanten, analoog aan een 2D elektronengas (c=1).
Een kristal alleen is echter niet voldoende om golven op te sluiten. De interne structuur van het kristal moet specifiek zijn afgestemd op de gewenste toepassing. Om het nog ingewikkelder te maken zijn er oneindig veel mogelijkheden voor deze structuur. Er zijn namelijk oneindig veel denkbare bouwstenen en ordeningen in het kristal. Tot nu toe moesten wetenschappers en ingenieurs die golven wilden opsluiten, vertrouwen op hun intuïtie, giswerk en dure proefondervindelijke experimenten.
Generieke aanpak
In hun artikel in Physical Review Letters presenteren de Twentse onderzoekers een robuust analyse-instrument dat voorspelt hoe golven in een kristal worden opgesloten, met alleen de structuur van het kristal als input. Eerste auteur en promovendus Marek Kozon MSc legt uit: "Een belangrijke parameter in onze analyse is een door ons uitgevonden 'opsluitingsdimensie'. Deze beschrijft de opsluiting voor elke mogelijke golf." COPS-groepsleiders prof. dr. Willem Vos en prof. dr. Ad Lagendijk voegen daar enthousiast aan toe: “We werden enthousiast toen we uit gesprekken met Marek begrepen dat onze methode niet alleen betrekking heeft op klassieke golven zoals geluid en licht, maar ook op quantumgolven zoals elektronen in minuscule nanostructuren.” Op basis van de nieuwe kennis kunnen de ontwerpers van kristallen nu profiteren van nieuwe ‘vuistregels’ voor specifieke toepassingen, met als resultaat sterk vereenvoudigde en dus efficiënte ontwerpprocessen. MACS-groepsleiders dr. Matthias Schlottbom en prof. dr. ir. Jaap van der Vegt voegen daaraan toe: "Onze resultaten zijn relevant voor efficiënte informatieverwerking in nieuwe fotonische en elektronische chips die toekomstige slimme steden zullen bevolken."

Figuur 2: Opsluitingsanalyse van een 2-dimensionaal quantumkristal voor elektronen in de halfgeleider hexagonaal boor-nitride met een stikstofvacature. (a) Dispersierelaties van het kristal. (b) Verhouding tussen het opsluitingsvolume en de opsluitingsenergie berekend voor elke voortplantingsband van golven. Rode punten komen overeen met banden in het kristal met grootte N = 5, en zwarte punten stellen het kleinere referentiekristal N0 = 3 voor. Met de toegenomen grootte bewegen banden met c=2 opsluiting naar beneden en banden met c=0 naar boven in de grafiek en zijn dus duidelijk te onderscheiden. Door de geometrie van de golfopsluiting blijken er geen c=1 banden te zijn.
Dit onderzoek is gedaan in de groepen Complex Photonic Systems (COPS) en Mathematics of Computational Science (MACS), beide onderdeel van UT's MESA+ Institute for Nanotechnology. Het artikel 'Scaling theory of wave confinement in classical and quantum periodic systems', van Marek Kozoň MSc, prof. dr. Ad Lagendijk, dr. Matthias Schlottbom, prof. dr. ir. Jaap van der Vegt en prof. dr. Willem Vos, is in oktober 2022 gepubliceerd in Physical Review Letters.
Ondersteuning
Het werk wordt ondersteund door het Shell-NWO/FOM programma "Computational Sciences for Energy Research" (CSER), door het NWO-TTW Perspectief programma P15-36 'Free-form scattering optics' (FFSO), door de NWO Open Competitie ENW-GROOT "Self-Assembled lcosahedral Photonic Quasicrystals with a Band Gap for Visible Light", en MESA+ sectie Applied Nanophotonics (ANP).
Publicatie op het internet
Het artikel "Scaling theory of wave confinement in classical and quantum periodic systems", door Marek Kozoň, Ad Lagendijk, Matthias Schlottbom, Jaap van der Vegt en Willem Vos, verschijnt in Physical Review Letters. De voor de publicatie gebruikte gegevens zijn beschikbaar in de openbare Zenodo database met DOI: 10.5281/zenodo.6783107.






