Statisticus Jasper de Jong verdiept zich al jaren in de mollenjacht. Als spelletjesfanaat, wiskundige en Wie is de Mol?-fan heeft hij een aantal inzichten uit de kansberekening toegepast op het popularie TV-programa.
Jasper kan bij verschillende spelsituaties de kans berekenen dat iemand de mol is. Anders dan bij de meer sociale oplossingmethodieken geeft deze berekening een hard getal. Bovendien is deze methode minder beïnvloedbaar door de spelleiding, die er natuurlijk alles aan doet om de kijker en de diverse molprofeten op het verkeerde been te zetten.
De wiskunde die er voor wordt gebruikt is de stelling van Bayes. Deze wiskundige stelling geeft de kans op een gebeurtenis, op voorwaarde dat een andere gebeurtenis plaatsvindt.
Neem de spelsituatie waarbij twee kandidaten uit het spel verwijderd worden en twee spelers niet kunnen afvallen, want zij hebben een vrijstelling. De overige vier dus wel, waar er twee van overblijven.
Voordat het oordeel wordt uitgesproken hebben alle zes kandidaten een bepaalde kans de mol te zijn, en die verandert uiteraard nadat de twee afvallen. Soms voelt dat logisch, soms gaat dat tegen de intuïtie in.
De stelling van Bayes ziet er als volgt uit:
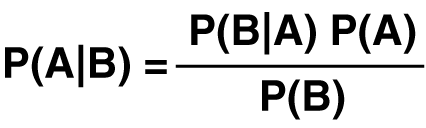
- P(A|B) is de kans dat situatie A optreedt gegeven dat situatie B optreedt
- P(B|A) is dan de kans dat situatie B optreedt gegeven dat situatie A optreedt
- P(A) is de kans dat situatie A optreedt ongeacht situatie B
- P(B) is de kans dat situatie B optreedt ongeacht situatie A
Patrick en Ron vallen af, dat zien we in de aflevering en is dus de gegeven situatie B. Hoe groot is dan de kans dat Peggy de mol is (situatie A | gegeven situatie B)? Met de stelling van Bayes is dat te berekenen door uit te gaan van het omgekeerde (hoe groot is de kans dat Patrick en Ron afvallen als Peggy de mol is) en de kansen P(A) en P(B).
Met die gegevens berekent Jasper dat de kans dat Peggy de mol is is gestegen van 1 op 6 naar 1 op 3. Een twee keer zo grote kans dus! En een grotere kans dan de verwachte 1 op 4 aangezien er nog vier kandidaten over zijn.
Bekijk de video voor preciezere berekeningen en voor nog meer situaties. Wat is bijvoorbeeld de kans dat Tygo de mol is?





