Thiago Dragman (2019)
Link to report in the repository: https://essay.utwente.nl/77888/
SUMMARY
Vibration-based Structural Health Monitoring (SHM) techniques are effective for detecting fatigue damage in structures by assessing changes in the dynamic behavior. When it comes to structures that exhibit significant nonlinear dynamic behavior, general SHM methods are not able to adequately describe the occurring dynamical phenomena. Furthermore, previous studies have shown that for flexible structures, changes in nonlinear system parameters were more sensitive to damage precursors than changes in linear system parameters. These facts suggest that a proper understanding of nonlinear dynamic properties is of high importance within SHM.
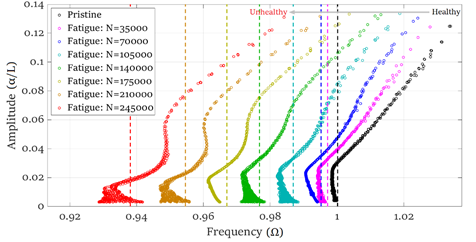
Figure 1: Backbone curves over various fatigue cycles.
This work identifies changes in the nonlinear dynamic behavior of cantilever beams over various stages of fatigue cycles by employing an experimental and analytical approach. The main aim was to investigate to what extent the monitoring of nonlinear dynamic system parameters can result in improved tracking of precursors to damage.
Experiments were carried out to characterize linear and nonlinear system parameters of Al7075-T6 cantilever beams. The dynamic characterizations included sine-sweep excitation (forced) and free vibration (transient). For each characterization, tests for the nonlinear and linear region were conducted. A signal processing approach was applied to convert the experimental data into useful results, such as backbone curves (see Fig. 1) and damping skeletons. By employing fatigue testing, the results were correlated to different levels of component health.
An analytical approach was carried out to develop the equation of motion (EoM) and to model the dynamic response. Techniques applied to derive the EoM include Nonlinear Euler-Bernoulli and the Assumed Modes method. The dynamic response was modeled using the Harmonic Balance method, the Method of Averaging and numerical methods (Runge-Kutta).
KEY RESULTS
- Backbone curves, which plot the system frequency versus the amplitude of vibration was obtained and correlated to various fatigue cycles (see Fig. 1). The shape of these curves showed significant changes for increasing fatigue cycles.
- Various nonlinear dynamic parameters were obtained and the sensitivity was compared to linear parameters. For some nonlinear parameters increased sensitivity was apparent (for example see Fig. 2).
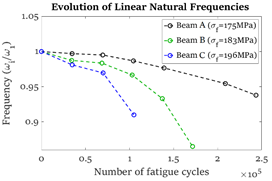

(a) (b)
Figure 2: Evolution of (a) linear frequencies and (b) bend point amplitude (nonlinear).
