Aim: develop a geometry-driven tool for multiscale modelling of composite materials based on elastomers, which would allow predicting the behaviour of new materials without conducting many experiments.
Nanofiller reinforced polymer composites in recent years composite materials have been used in almost all areas of industry and science, like transport, aerospace, etc. To manage such material creation and their application, new methods of material analysis techniques and optimisation of well-known are needed. The mechanical material modelling is used for that matter to predict behaviour of the material under load when a full-scale experiment is impossible or requires much experimental repetition.
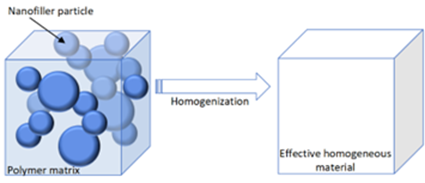
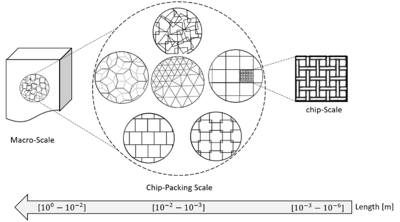
The polymer composites modelling can be done by the homogenization approach, the principle of which is to replace a heterogeneous medium with homogeneous one with effective properties. Since, the underlying geometry determines the mechanical behaviour of the composite, geometry-driven model is proposed.
In the context of this project, on macroscale, the material is considered a homogeneous structure (scale of observation more than 1 mm). The mesoscale for elastomer-based composite is the observation level, where the polymer matrix considered as a homogeneous material with the filler particles network (scale of observation about 1 mm). The nanofiller forms a network inside the polymer mass made from aggregations and agglomerations. Such a structure can be generated fractally. The microscale is represented by a lower observation level: polymer chains with cross-links, where the polymer chain size is about 0.5 nm width and 200nm long.
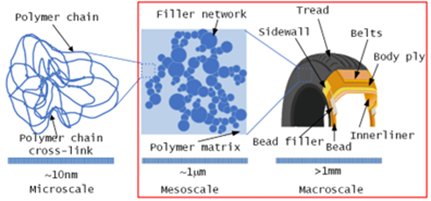
This study only considers the mesoscale and macroscale of the material in question. Mesoscale modelling includes modelling the behaviour of these individual elements, followed by modelling the geometry of the structure. Such an engineering problem is reduced to describing the mechanical state of the body using constitutive equations for each material separately. A nanofiller such as Carbon Black is assumed to be a linear elastic material, while elastomer matrix can be described with the strain energy potential of the Ogden model.
The nanofiller forms a network inside the polymer mass made from aggregations and agglomerations. Such a structure can be generated fractally. This generation of a filler network inside a homogeneous elastomer matrix material allows to model the material at the mesoscale. The transition to the macroscale can be done using the multigrid method for homogenization.
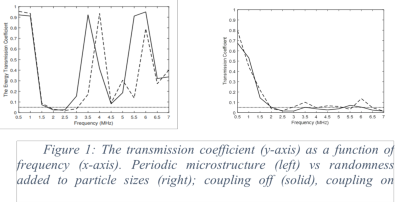
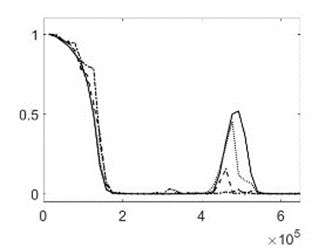
The generally accepted approach for describing the deformations of elastomers is using the finite element method.
However, obtaining a practical convergence of the numerical solution by the finite element method when performing a non-linear simulation of a hyperelastic material can be a non-trivial task. Hyperelastic material behaviour analysis requires a mesh to consider the expected deformations of the material. Fine mesh in problems with hyperelastic materials reduces the accuracy of calculations since small finite elements in high deformation zones experience significant shape distortions.
Therefore, the development of new approaches based on mesh resizing can make it possible to solve such problems for hyperelastic materials more efficiently. In recent years, the so-called Multigrid method (MG) has become one of the practical and universal methods for solving systems of equations.
Multigrid method (MG) is the practical method for solving systems of equations to accelerate the convergence of a basic method. In case of MG the iterative process requires significantly fewer computational power to bring the accuracy to the required limits.

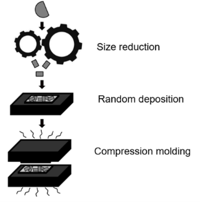 Mechanical recycling techniques use grinding techniques to comminute waste materials and create recycled products in smaller size, named flakes (Fig. 1). During the compression molding process, flakes are dropped into the mold randomly. It creates a complicated stochastic meso-structure that makes it difficult to simulate the mechanical behavior. To predict the mechanical properties of recycled composites, large number of test specimens is required, which is time consuming and costly. Therefore, an accurate numerical model to predict the mechanical characteristics of recycled composite will be required.
Mechanical recycling techniques use grinding techniques to comminute waste materials and create recycled products in smaller size, named flakes (Fig. 1). During the compression molding process, flakes are dropped into the mold randomly. It creates a complicated stochastic meso-structure that makes it difficult to simulate the mechanical behavior. To predict the mechanical properties of recycled composites, large number of test specimens is required, which is time consuming and costly. Therefore, an accurate numerical model to predict the mechanical characteristics of recycled composite will be required.