Duration: 2024-2028
Funding: NSM
ABOUT THE PROJECT
In my research project I am exploring how machine learning (ML) can enhance the performance the Finite Element Method (FEM) in nonlinear solid mechanics through model order reduction. I do so by developing a hybrid sub-structuring approach that leverages machine learning trained “intelligent macro elements”. This method offers a versatile and generalizable framework applicable to various scenarios, with the aim of reducing computational complexity without sacrificing accuracy. Target applications include forming processes and other problems involving contact, as well as geometrical and material nonlinearities.
GOALS
Various numerical strategies have already been developed to reduce complexity, such as reduced basis methods. While effective for linear problems, these approaches face significant limitations when applied to nonlinear models. Similarly, a number of research studies have explored the use of machine learning to replace constitutive material laws and the numerical integration steps in conventional FEM.
The hybrid ML- FEM approach I am exploring in this research project, combines the strengths of classical FEM dimensionality reduction methods (e.g. static condensation) and the robust and efficient prediction capabilities of machine learning, especially for nonlinear problems. The core idea is to integrate an intelligent macroelement into the FEM model by learning the (nonlinear) relationship between boundary nodal displacements and forces for a given loading scenario. This relationship is obtained through machine learning, after a dedicated training phase, and allows the intelligent macroelement to replace a detailed internal mesh while maintaining accurate global behavior within the FEM simulation.
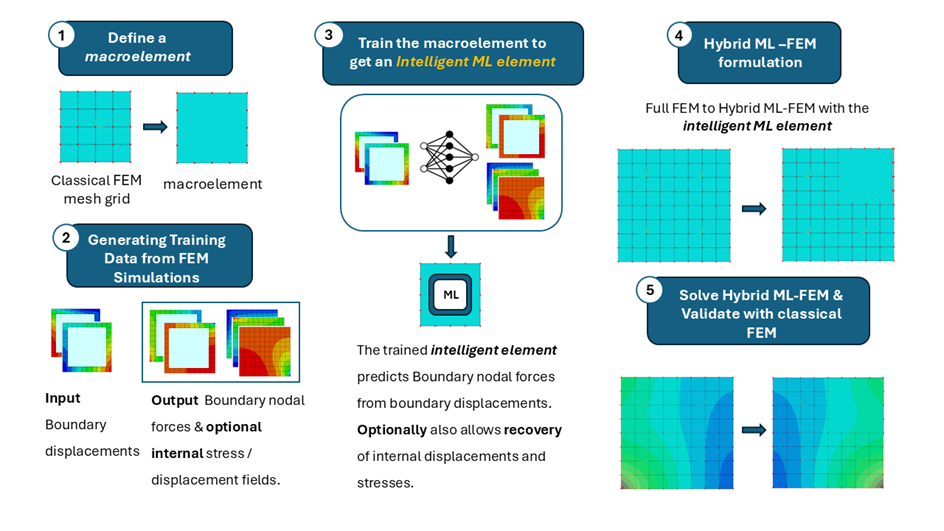
Figure 1: Model order reduction hybrid ML-FEM framework for nonlinear solid mechanics


