
The biaxial tester is part of the Mechanical Testing Laboratory.
Introduction
To improve the current status of sheet metal forming simulations, ongoing research in the field of, amongst others, material modeling, springback, tool compensation and optimization are required. Commonly however, all these advanced methods seem to consume more CPU time than their predecessors. The impressive evolution of computers with multiple and stronger processors has also contributed to the use of these algorithms. Still, all this progress comes at a price; not every user wants to use all the advanced options, because they can be too expensive (commercial software), or in the case of more advanced material models, the user needs to understand the model to apply it correctly. Besides, sophisticated models require sophisticated experiments to determine the material parameters, which in general is time consuming and thus expensive. In material models the trend is currently to incorporate strain path dependency in the model, making the modeling more complex and requiring more experiments for parameter fitting.
In this research a biaxial testing device is used to examine the strain path effects. With this equipment two different deformation modes can be subjected to the sample, such that a strain path change occurs in the material. The advantage of this equipment over the regularly used method is that stresses and strains are recorded during the strain path change. Moreover, the equipment enables to vary the strain path change from very gradual to instantaneously. The strain path effects can be examined, dependent on the smoothness of the transition from the first to the second deformation mode. With these results a criterion for the sharpness of the strain path change can be derived, such that the strain path change indicator can be parameterized.
Experimental device
To investigate the effects of strain path changes on the mechanical response, an in-house developed biaxial testing device is used. It consists of a uniaxial testing device and a sub frame mounted between the crossbars. The sub frame accommodates the actuator for the shear deformation whereas the uniaxial frame controls the tensile deformation. The advantage over a biaxial tester with cross-shape samples is that the simple shear–tension layout allows to determine full stress–strain curves with large strains. The figure below shows a drawing of a sample and the loading directions of the clamped parts of the sample.
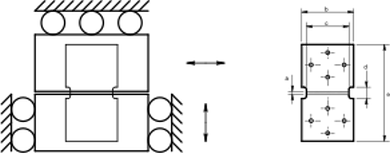
The height to thickness ratio is relatively small to avoid wrinkling in simple shear tests, whereas the large width to height ratio results in a plane strain condition in transverse direction in a tensile test. It is noticed that the transverse stress cannot be measured, so only the simple shear and tensile stress are known and principal stresses cannot be calculated. To determine the deformations in the sample an optical system is used. 16 black silicon dots on the surface of the deformation zone are tracked with a camera and the software calculates the coordinates of the individual dots. With this information the strains are (real-time) calculated. Stresses are easily calculated via the force signals and the dimensions of the sample.
In the current test equipment the stiffness plays a crucial role. This shows itself in the determination of strains, here the positions of the actuators do not give accurate results and therefore the optical system is used. Moreover, the elasticity of the machine is interfering with the actual tests in applying strain path changes to a material. The relation between the controls of the machine and the actual strain in the material is not a direct relation, but is also a function of the stiffness of the machine. In the applied strain path changes, the stress state translates over the yield surface and hereby the tensile stress is reduced. Since the test equipment itself is also elastically stretched in the tensile test, the release of force in this direction reduces the elongation in the test equipment. Consequently, an extra deformation is applied to the sample. A maximum increase of 7 % tensile strain was found after the strain path change. An algorithm was developed to compensate for this effect and implemented in the software. Moreover, by changing the parameters of this algorithm the strain path changes can be made gradually or sharp.
