We give here a couple of examples of methodological developments we have carried out in recent years.
Efficient interatomic forces and more
Very recently, we have developed a simple formalism to compute efficiently the derivatives of a multi-determinant Jastrow-Slater wave function, the local energy, the interatomic forces, and similar quantities needed in quantum Monte Carlo. Without the need for algorithmic differentiation, we obtain remarkable efficiency in the computation of the interatomic forces or the optimization of the orbital parameters as shown in the figure below, where the cost of computing the forces of a system as large as C60H62 is only a few times larger than the cost of evaluating the energy.
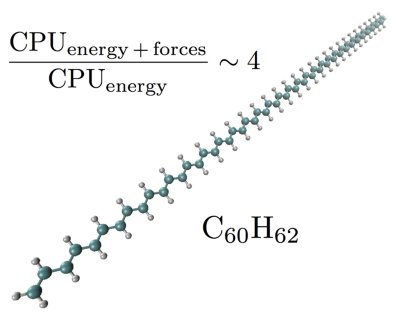
C. Filippi, R. Assaraf, and S. Moroni, Simple formalism for efficient derivatives and multi-determinant expansions in quantum Monte Carlo, J. Chem. Phys. 144, 194105 (2016).
Local correlation description of ground and excited states
The accurate, yet affordable, computation of excited states in large molecules remains a challenge in computational chemistry. Using the familiar concepts of local orbitals and Lewis resonance structures, we have recently proposed a new class of accurate many-body wave functions specifically designed for the efficient treatment of excited states in quantum Monte Carlo. Key ingredients are a coupling scheme to correlate electrons within domains of local orbitals and the use of multiple structures in an over-complete orbital set. These concepts have led to modular, flexible wave functions of increasing complexity that scale linearly with system size.
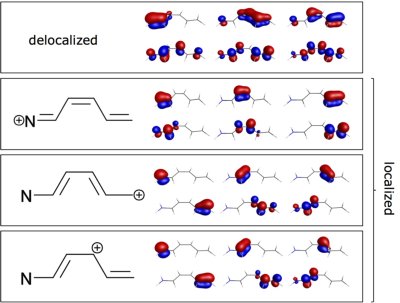
H. Zulfikri, C. Amovilli, and C. Filippi, Multiple-resonance local wave functions for accurate excited states in quantum Monte Carlo, J. Chem. Theory Comput. 12, 1157 (2016).
