A scattered electron will have a different momentum compared to its initial state. The interference of incoming and scattered electrons at point impurities gives rise to a standing wave pattern in the local density of states. Only electrons near the Fermi level participate in this process. This effect, called quasiparticle interference, is a beautiful example of the particle-wave duality, as it involves electrons that interfere with itself as a wave. The observed scattering pattern contains information on the Fermi surface contour and on the electronic band structure of the material. The 2D FFT of the scattering pattern can provide the distribution of scattering wave vectors in reciprocal space.
will have a different momentum compared to its initial state. The interference of incoming and scattered electrons at point impurities gives rise to a standing wave pattern in the local density of states. Only electrons near the Fermi level participate in this process. This effect, called quasiparticle interference, is a beautiful example of the particle-wave duality, as it involves electrons that interfere with itself as a wave. The observed scattering pattern contains information on the Fermi surface contour and on the electronic band structure of the material. The 2D FFT of the scattering pattern can provide the distribution of scattering wave vectors in reciprocal space.
Quasiparticle interference is a beautiful example of the particle- wave duality, as it involves electrons that interfere with itself as a wave
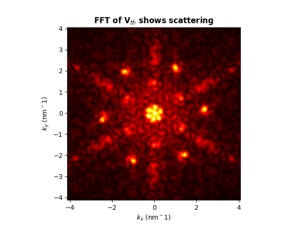
Because graphene consists of two triangular lattices which are intertwined the symmetry of the carbon atoms is destroyed. This results in a property called pseudospin. Pseudospin needs to be conserved in a scattering event affecting the available scattering wave vectors. By shifting the Fermi level, the influence of the dispersion relation on the scattering events can be investigated. In addition, information about the chirality of Dirac electrons and the topological properties of the wave functions can be obtained. Scattering effects in graphene have a profound impact on electron transport properties in graphene with suppression (enhancement) of weak localization according to the presence (absence) of time-reversal symmetry, respectively.
