For background information on the topic as a whole, scroll to the end of this page.
Available Project Proposals
If you are interested in the general topic of Quantitative Verification, or if you have your own project idea related to the topic, please contact us directly. Alternatively, you can also work on one of the following concrete project proposals in various subfields of quantitative analysis:
Modelling Language Technology
Modelling languages are similar to programming languages, yet different. We offer topics related to various aspects of our modelling language compilers.
- Adventure Games with Formal Guarantees (Moritz Hahn)
Adventure Games with Formal Guarantees
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
Adventure games are strongly story-based video games. The player controls the protagonist, steering its actions, so as to drive forward the story. The user interface often allows interactions of the form “do <verb> with <object 1> together with <object 2>” or similar. This type of game has been quite popular for a while, but faced a decline by factors such as lack of motivation to for the player to play a game more than once, high effort of drawing graphics, and high cost of developing the storyline. The latter results because the designers have to take into account the many different ways in which a player might interact with the environment. Typically, it is considered a design error if it is possible to reach a situation in which the player is stuck and not able to reach the goal of the game anymore.
(https://www.gog.com/en/game/flight_of_the_amazon_queen)
In this project, you are going to apply formal methods to ease the development of adventure games. The idea is to develop a domain-specific language (SDL) which describes the possible interactions of the protagonist with the environment. The SDL shall be transformed into the input languages of general model checkers, such as e.g. the input language of SPIN. Desirable properties shall be expressed by a property specification language, which could be translated into a formal logic. For instance, never reaching a situation in which one is stuck could be expressed as the CTL formula “AG (EF won)”. This way, it will be possible to check whether the desired properties indeed hold.
If you are interested in this project, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
- Grid-world Scenario Editor (Moritz Hahn)
Grid-world Scenario Editor
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
Grid-world scenarios are a type of formal models which are often used to evaluate or demonstrate model checking or reinforcement learning algorithms. The scheme is such that one or agents are positioned in a cell of a fixed grid. Each step, they can move into one of four directions. Depending on the property under consideration, they might have to perform certain tasks there. For instance, in the scenario sketched below, we might ask whether it is possible for the robot to distribute coffee infinitely often from the coffee room to the other three rooms.

In this project, you are first going to perform a literature study about the common features of such grid-world scenarios. Afterwards, you are going to implement an editor supporting a well-justified set of such features. Your editor shall have an export functionality, so as to be able to export at least to the JANI format. The export shall be performed in such a way that model checkers reading the model can perform analyses efficiently and that you can compare results from the literature with your implementation.
If you are interested in this project, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
- Queueing System Editor (Moritz Hahn)
Queueing System Editor
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
Queueing systems are a type of formal models which are often used to evaluate analysis tools for continuous-time Markov chains and related models. Queueing systems consist of several connected queues, each of which can handle a (finite or infinite) number of customers. Once a customer has been handled by a certain queue, it either leaves the system or moves to the next queue.
As an example, consider the system below: Customers enter the system with rate a. With probability 0.7, they move to queue 1 (which has a capacity of 4), with probability 0.3 they move to queue 2 (which has a capacity of 3). From queue 1, they move to queue 3 (which has an infinite capacity) with rate b, and from queue 2 they move to queue 3 with rate c. From queue 3, customers leave the system with rate d.
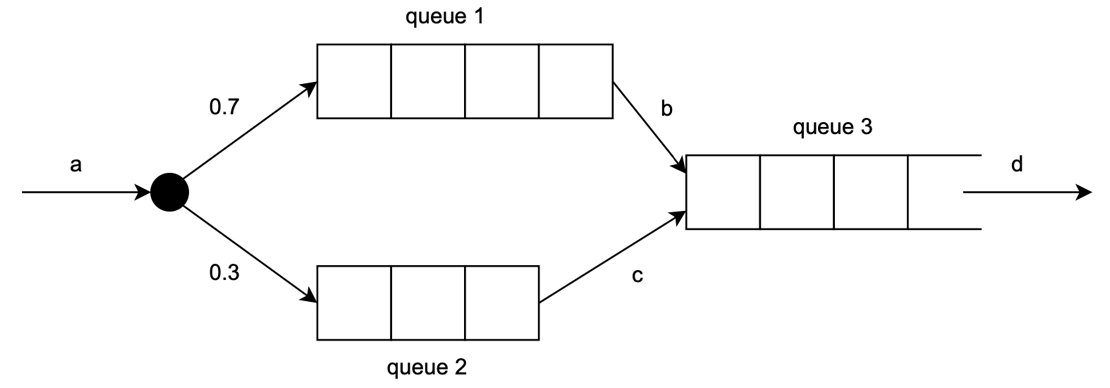
In this project, you are first going to perform a literature study about the common features of such queueing systems. Afterwards, you are going to implement an editor supporting a well-justified set of such features. Your editor shall have an export functionality, so as to be able to export at least to the JANI format. The export shall be performed in such a way that model checkers reading the model can perform analyses efficiently and that you can compare results from the literature with your implementation.
If you are interested in this project, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
Probabilistic Verification
Probabilistic model checking and statistical model checking compute optimal probabilities, expected values, and strategies for Markov models. You can implement new algorithms, combinations of methods, or improve performance.
- Algorithmic collusion for omega-regular properties in grid-world scenarios (Janusz Meylahn, Moritz Hahn)
Algorithmic collusion for omega-regular properties
in grid-world scenariosSupervisor: Janusz Meylahn (j.m.meylahn@utwente.nl), Ernst Moritz Hahn (e.m.hahn@utwente.nl)
Consider a scenario of multiple agents, each of which is following their own interest and is using reinforcement learning (RL) to maximize their profit. Under certain conditions, collusion may occur, that is, the RL algorithms might implicitly negotiate contracts with other agents.
In this proposed thesis, you are going to research collusion in scenarios where agents operate on a grid-world and follow an omega-regular objective. Omega-regular properties are properties which can be described using omega-regular automata or logics. They can describe more complex behaviours than reward signals. For instance, consider the example below:

The first robot tries to distribute coffee from the coffee room to the other three rooms. This behaviour can be described as Pmax [G (F coffee ∧ XF room1 ∧ XF room2 ∧ XF room3)]. The second robot wants to move between two rooms, expressible as
Pmax [G (F room1 ∧ F room2)]. To efficiently perform these tasks, profit from negotiating with each other, so as to avoid each other’s path. It would be convenient for each robot to ignore the other robot completely rather than moving out of the way, because in this way it might be able to distribute coffee more quickly. However, in this case, the other robot would reciprocally do the same, if according RL algorithms are used.
There is an active area of using RL for handling omega-regular properties. The novel aspect of this thesis is the combination with collusion. The challenges of this thesis are
- implementing appropriate transformations from omega-regular properties to rewards,
- implementing appropriate 2-player RL algorithms on top of the above,
- evaluating the results, and
- providing an outlook for a theoretical foundation of these results.
- Genetic Algorithms for Controller Generation of Markov Decision Processes (Moritz Hahn)
Genetic Algorithms for Controller Generation of Markov Decision Processes
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
Markov decision processes (MDPs) are a modeling formalism which applies to a wide range of systems. MDPs feature both control as well as stochastic behavior. For instance, consider the robot scenario below.

At each point of time, the robot can move in one of four directions. With a probability of 0.3, it moves up two fields, and with a probability of 0.7, it moves up one field. Assume that we want to steer the robot in such a way that it distributes coffee from the coffee room to all the other three rooms. For doing so, we have to resolve the nondeterministic choices in such a way that the property is fulfilled. We can obtain controllers which do so, by using methods such as reinforcement learning or model checking. These methods often work well, but they have the disadvantage that the decisions made are often hard to understand.
In this project, we target at synthesizing understandable controllers in terms of guarded command programs (GCP). A GCP consists of multiple commands, each with a certain guard. A command can be executed in a situation in which its guard is fulfilled. For instance, a controller such as
[ ] blocked_up ∧ right_free → move_right
[ ] blocked_down ∧ left_free → move_left
…
would try to move right if the robot can move right but not up, and move left if the left field is free but the field down is blocked. We aim at automatically deriving such controllers using genetic algorithms. The challenges are
- Implementing the infrastructure to work with guarded commands,
- implementing the connection to a model checker, e.g. the Modest model checker,
- developing good selection criteria, and
- developing ways to mutate a given GCP.
If you are interested in this project, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl). If the implementation for this project is going to be integrated into the Modest model checker, you can consult Arnd Hartmanns (a.hartmanns@utwente.nl) for implementation-related questions.
- Genetic Algorithms for Controller Generation of Understandable Bomberman Controllers (Moritz Hahn)
Genetic Algorithms for Controller Generation of Understandable Bomberman Controllers
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
Bomberman is a game series in which players target at being the last remaining player in the game, using bombs to blow up their opponents.
(https://github.com/bjaraujo/Bombermaaan)
The idea of this proposal is to steer Bomberman agents using guarded command programs (GCP). A GCP consists of multiple commands, each with a certain guard. A command can be executed in a situation in which its guard is fulfilled. For instance, a controller such as
[ ] bomb_up ∧ right_free → move_right
[ ] bomb_left ∧ left_free → move_left
…
would try to avoid a bomb by moving to a direction which is not blocked.
We target at automatically deriving efficient controllers using genetic algorithms. The idea is to use Bomberman as a playground to develop means of synthesising controllers which are
- easy to understand by humans,
- easy to implement,
- depending on limited information (e.g. limit the sight of the player), and
- generally applicable (work well for several scenarios).
The challenges are
- implementing a suitable version of Bomberman,
- writing an interpreter to steer the agents according to GCP,
- developing good selection criteria, and
- developing ways to mutate a given GCP.
If you are interested in this topic, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
- Increase Your Floating-Point Precision When Stuck (Arnd Hartmanns, Bram Kohlen, Peter Lammich)
Supervisors: Arnd Hartmanns, Bram Kohlen, Peter Lammich
We recently developed variants of the interval iteration algorithm, which is used for the iterative numerical computations in probabilistic model checking, that use correct rounding in all floating-point computations. Now these algorithms are free of floating-point errors, but now they sometimes tend to get "stuck" at a fixpoint due to rounding before reaching the desired error specified by the user. In this project, you will investigate – devise, implement, and benchmark – modifications of this approach that, instead of giving up, increase the floating-point precision (in hardware or in software, e.g. via the MPFR library).
- Interactive State Elimination (Moritz Hahn)
Interactive State Elimination
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
State elimination is a method to analyse properties of Markov models, such as Markov chains or Markov decision processes. The idea is to systematically remove states of the model, while keeping the measure (e.g. probability that a set of states is reached) of interest as it is. For instance, in the model sketch below
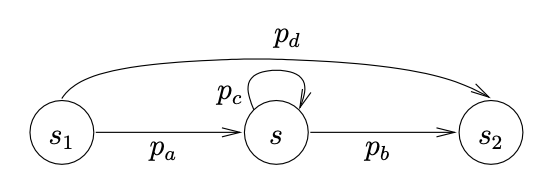
we can eliminate state s so as to obtain the model below in which the probability to reach certain sets of states from the other states are still the same, even though state s is not present anymore.
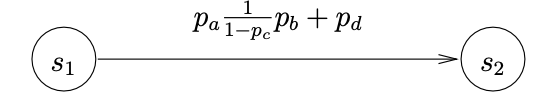
By this elimination process, the model eventually reaches a form from which the measure of interest can be obtained directly. Even though in the end the number of states will be very small, it may happen that the size of the state space actually increases in the elimination process before shrinking again.
In this project, you are going to develop a tool in which state elimination can be performed interactively. The purpose of developing such a tool is to
- allow to experiment with the best elimination order for certain types of models and to
- Illustrate the usage of state elimination to researchers entering the area.
The technical implementation of this project is up to you. If you want to implement this as a web application, you could use the tool UTML which is an interactive diagram editor developed at the University of Twente.
If you are interested in the topic, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
- Safe Rounding in Iterative Numeric Algorithms (Arnd Hartmanns, Bram Kohlen, Peter Lammich)
Supervisors: Arnd Hartmanns, Bram Kohlen, Peter Lammich
We recently developed variants of the interval iteration algorithm, which is used for the iterative numerical computations in probabilistic model checking, that use correct rounding in all floating-point computations. Similar ideas should be applicable to similar algorithms like sound or optimistic value iteration; and they should work for expected rewards, too, where we so far only implemented them for reachability probabilities. In this project, you will pick one or two algorithms that do not yet have a correctly rounding implementation, think about which rounding mode needs to be applied at which places, implement the result, and benchmark it.
(Probabilistic) Timed Automata
Timed automata are an established way to model hard real-time systems. Probabilistic timed automata capture the combination of randomisation and real-time behaviour.
- Diagonal Digital Clocks (Bram Kohlen, Arnd Hartmanns)
Supervisors: Bram Kohlen, Arnd Hartmanns
The digitals clocks technique is one way to model-check probabilistic timed automata (PTA): models of real-time systems with randomised choices. It is commonly applied to diagonal-free PTA only, where clock variables cannot be compared to each other. However, the underlying correctness proof does not require this restriction. You will devise an approach that preserves all the information necessary to decide diagonal clock constraints and implement it in the Modest Toolset.
- Modelling medical protocols with UPPAAL (Rom Langerak)
Supervisor: Rom Langerak
It is difficult to reason about medical diagnostic and treatment protocols: they usually consist of many processes, and timing, cost, effectiveness, and uncertainty play a complex role. We are therefore modelling and analyzing such protocols using the timed-automata-based tool UPPAAL. Examples of past work include treatment of prostate cancer (with BMS), side effects of immunotherapy (with NKI), and tooth wear monitoring (with ACTA).
Assignments (to be formulated in agreement with the interests of the student) may include practical modelling and analysis, theoretical research, and tool development.
Other Topics
- Evaluating state elimination (Moritz Hahn, Matthias Volk)
Supervisor: Ernst Moritz Hahn, Matthias Volk
State elimination is a method which works as follows: Starting with the original state-space or a Markov chain, states of the model are systematically removed, while making sure that the property (e.g. probability that a bad state is reached) is maintained. In the end, this way, the model reaches a form from which it is trivial to obtain the property one is interested in.
This project is about evaluating for which models state elimination works particulary well and in which order states shall be eliminated, and why. Depending on agreement with the candiate, the focus could be
- more on the theoretical side, considering structural properties of model classes for which state elimination works well as well as a good/optimal elimination order, or
- could be more on the practical side, implementing a tool in which one can either manually specify the order in which to eliminate states, use a scripting language (JavaScript, Lua, etc.) to decide about the order of elimination or integrate new elimination orders in existing tools.
- Evaluating Student Solutions for Automata (Moritz Hahn)
Evaluating Student Solutions for Automata
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
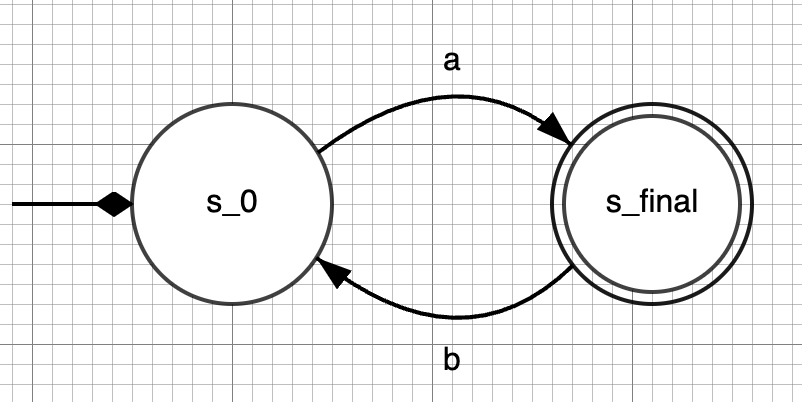
As part of the module Languages & Machines (L&M), students are required to design automata with a given language. For instance, they might be given the regular expression E = (ab)* and be asked to design a finite automaton the language of which is L(E). A possible correct solution is the following automaton:
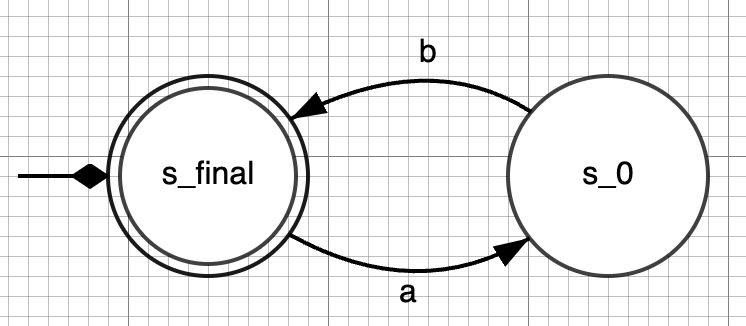
However, students might come up with incorrect solutions such as the following one, in which the accepting and non-accepting states are switched:
In this project, you are going to evaluate a tool to provide feedback - formative and/or summative - to student solutions, so as to improve the understanding of automata constructions for the L&M module. The challenges here are
- How good or how bad is an incorrect solution - in terms of points?
- How to demonstrate to the student how an incorrect solution could be fixed?
- How to take into account that there is no unique solution, but infinitely many ones?
The technical realisation of the tool is up to you. However, we require the tool to be web-based, so as to be easily accessible to the target audience. We suggest to base it on the diagram editor UTML which is developed at the University of Twente.
If you are interested in this project, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
- Gamification for Deductive Systems (Moritz Hahn)
Gamification for Deductive Systems
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
Deductive systems are a proof method to show that a formula of a formal logic is valid. That is, if it is possible to prove that a formula is true using a correct deductive system, the formula is true under any interpretation. The proofs constructed using deductive systems are trees, such as the following one for the formula (∀ x. p(x) ∨ ∀ x. q(x)) → ∀ x. (p(x) ∨ q(x)):
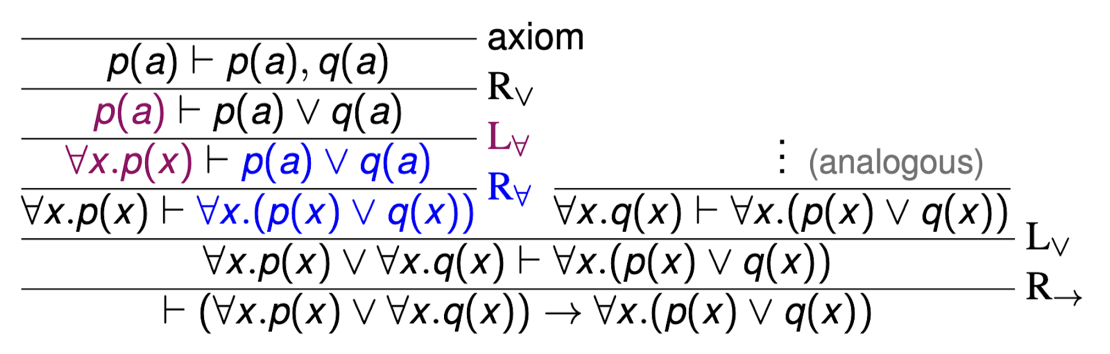
Using deductive systems is an important learning goal in the MSc course Advanced Logic. Unfortunately, students find using such systems to prove a concrete formula very hard. This holds in particular for those of the so-called Hilbert type.
In this project, you are going to develop a video game in which students build such trees interactively, such that future students have a better way of training on a larger number of examples than doing them purely by pen-and-paper on a limited example set. The objectives and challenges for this thesis are thus
- How to automatically generate formulae with an appropriate difficulty level?
- How to let the student input proofs in an efficient way?
- How to grade partial solutions?
- How to provide motivating feedback to the student?
The technical implementation of such a game is up to you. We would however be able to provide some Lua-based infrastructure for working with formulae, such as parsing them, etc. If you are interested in this topic, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
- Hanoi Format Graphical Editor (Moritz Hahn)
Hanoi Format Graphical Editor
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
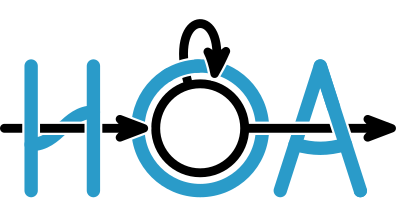
The Hanoi format (HOA) is a textual description of automata which describe omega-regular languages, that is, languages over infinite words. HOA is a text-based format, which allows to specify automata with different so-called acceptance conditions. All these automata can describe the same class of languages, but they might be fit for different applications, or they might allow for a more or less compact representation.
In this project, you are going to implement a web-based graphical editor using the diagram editor UTML which is maintained at the University of Twente. The challenges here are to
- study the literature to design a tool which behaves according to user expectations,
- input and output of the HOA format,
- positioning the states when reading from the HOA format,
- simulating the automata, and
- performing simple conversions from one automaton class to another one, e.g. conversions from Büchi automata to 2-color parity games.
An appropriate level of formal methods as well as software engineering and GUI design is required. However, the focus of the project may be one one or several of the points discussed, following negotiations with the student.
If you are interested in this topic, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
- Infinite Board Games (Moritz Hahn)
Infinite Board Games
Supervisor: Ernst Moritz Hahn (e.m.hahn@utwente.nl)
Infinite games are games in which a player wins if being able to fulfill an omega-regular property, that is to reproduce a certain behaviour infinitely often rather than fulfilling an objective which can be obtained in a finite number of steps. Such games often occur in the formal verification or synthesis of systems, e.g. when building a controller which is able to safely steer a system under possible behaviours of its environment. As an example, consider the situation below:

Here, two robots operate on a grid-world. At each point of time, they can move to one of four directions. With probability 0.1, they move one field, and with probability 0.9 they move two fields. The objective of the first robot is to distribute coffee to all coffee rooms, which can be expressed as the LTL formula
Pmax [G (F coffee ∧ XF room1 ∧ XF room2 ∧ XF room3)]. The objective of the second robot is to prevent this.
The objective of this project is to develop a type of board game in which the player is given an omega-regular property and is supposed to steer the agent in such a way that the property is fulfilled. The assumed challenges here are to
- implement an algorithm to check omega-regular properties,
- design the user interface; in particular, allowing the user to specify infinite sequences with finitely many interactions,
- writing the game in such a way that it is challenging and interesting.
If you are interested in this topic, please contact Ernst Moritz Hahn (e.m.hahn@utwente.nl).
- Modelling board games (Milan Lopuhaä-Zwakenberg)
Supervisor: Milan Lopuhaä-Zwakenberg
Board games are an easy-to-understand model of stochastic systems as they naturally contain sources of randomization (throwing dice, drawing cards, etc.). Existing work has already modelled some board games and puzzles as Markov models.
Research directions:
In this project, we aim to model a selection of popular board games as probabilistic models and analyse them via model checkers such as Storm. Possible candidates include:
- Monopoly
- Game of the Goose
- The Quacks of Quedlinburg
- Lost Cities
- Incan Gold
- Royal game of Ur
- Snakes and Ladders
You are free to consider board games or puzzles with randomization of your own liking.
Requirements
Interest in board games is very beneficial. It is useful but not required to have knowledge on Markov chains.
- Reproducing StoCharts (Moritz Hahn)
Supervisor: Ernst Moritz Hahn
Statecharts are a widely known flexible graphical modelling mechanism to describe behavioural aspects of models in UML. StoCharts [1-3] are a mechanism to enrich Statecharts with stochastic behavours, such as failure rates, unforseeable delays in actions performed, etc. In previous works, StoCharts have been used to analyse safety properties of train radio systems.
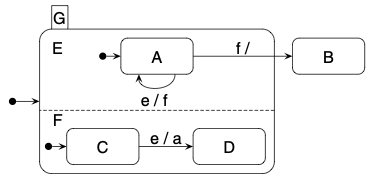
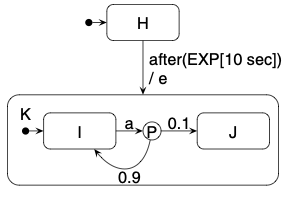
Statechart [1]
StoChart [1]
UTML is an editor developed at the FMT group of the University of Twente which allows draw graphs which have a formal semantics, such as deterministic finite automata, or fault trees. In particular, models created by UTML are easy to parse, because they are stored as JSON data.
The purpose of this thesis is to reproduce the results obtained from these works. For this, the idea is to
- Parse the UTML data to StoCharts
- Transform these StoCharts into the (also JSON-based) stochastic modelling language JANI
- Analyse these models with the Modest model checker
- Compare the results to the ones provided in the existing publications
References:
- [1] David N. Jansen, Holger Hermanns: Dependability Checking with StoCharts: Is Train Radio Reliable Enough for Trains? QEST 2004: 250-259
- [2] Holger Hermanns, David N. Jansen, Yaroslav S. Usenko: From StoCharts to MoDeST: a comparative reliability analysis of train radio communications. WOSP 2005: 13-23
- [3] David N. Jansen, Holger Hermanns: QoS modelling and analysis with UML-statecharts: the StoCharts approach. SIGMETRICS Perform. Evaluation Rev. 32(4): 28-33 (2005)
Contact



Background
Probability is everywhere in our daily lives and IT systems: as games of chance, as random events like device failures, or in randomised algorithms. Other systems show time-dependent behaviour or need to satisfy real-time requirements. Sometimes, timing and probabilities are intertwined, like in communication protocols, or we even need to consider quantities evolving according to physical laws such as a room's temperature or the water level in a buffer tank.
In FMT, we work with (extensions of) Markov chains, Markov decision processes, stochastic games, and timed automata to model such systems. We model real-life systems with UPPAAL, use fault trees as a graphical tool to think about failure probabilities, and develop the Modest Toolset to create, simulate, and verify formal models that include probabilities and timing.
We offer B.Sc. research projects related to probabilistic, timed, and hybrid verification topics: on case studies, modelling language and compiler improvements, algorithms for model checking and simulation, and connections with other languages or tools.
Prerequisites
- Basic probability theory and statistics (for probabilistic topics)
- Object-oriented programming experience
Related Modules
- Discrete Structures and Algorithms (automata and graph algorithms)
- Cyber-Physical Systems (modelling and verification with UPPAAL)
- Programming Paradigms (compiler construction)
