Als je een doos met Mikado-stokjes flink schudt, krijg je dan een verdeling van de stokjes die een beetje gelijkmatig verdeeld is? Dit raakt aan de klassieke paradox van Bertrand uit de wiskunde: dat is in het platte vlak al een lastig probleem, maar wat als je naar 3D gaat en ook nog eens precies wilt weten hoe groot de gaten tussen de stokjes – ‘koorden’ in de wiskunde – zijn? Dit wilden UT-onderzoekers van het MESA+ Instituut weten om nano-mikadodoosjes te kunnen ontwerpen voor fotonica. Zij bedachten een rekenmethode voor het kiezen van de koorden en bliezen denkbeeldige bolletjes op om de maat van de gaten vast te stellen. Het onderzoek is gepubliceerd in het journal Physical Review E.
Dat een bekende paradox uit de 19de eeuw weer opduikt bij het ontwerpen van innovatieve nanostructuren voor het manipuleren van licht, is bijzonder. Die paradox, van Joseph Bertrand, gaat over ‘koorden’, de lijnen die je kunt trekken tussen twee punten op een cirkel. Neem je een gelijkzijdige driehoek, teken je daar een cirkel omheen, hoe groot is dan de kans op koorden die lánger zijn dan de zijden van de driehoek? Bertrand beschrijft drie methoden die elk een ander antwoord geven. Hóe je de koorden kiest, blijkt uit te maken. Het was Edwin Thompson Jaynes die, bijna een eeuw later, een uitweg formuleerde uit de paradox. Hij stelt dat maar één van de drie methoden in staat is om de cirkel te vullen met koorden die ongeveer homogeen is. Op die manier lijkt het midden van de cirkel niet doorzichtiger dan de randen. De onderzoekers breidden die constructiemethode uit naar drie (en meer) dimensies. Ze kunnen daarmee allerlei ruimtelijke vormen opvullen met koorden die gelijkmatig verdeeld zijn.
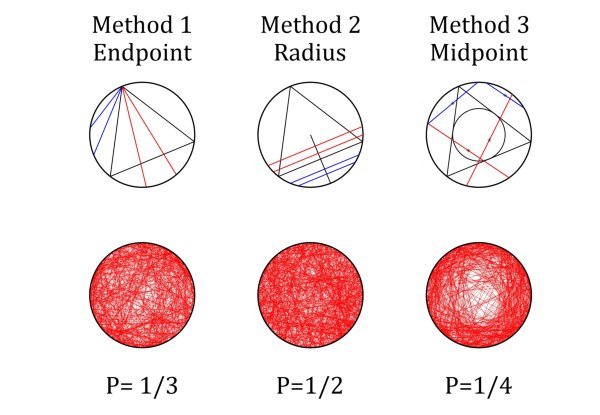
Bertrand's paradox. Cirkel rondom een gelijkzijdige driehoek: drie manieren om de cirkel te vullen met lijnen die langer zijn dan de zijden van de driehoek. Verbind twee willekeurige punten op de cirkelrand (1), kies een willekeurige straal en trek hierop loodrecht een lijn (2) of kies een willekeurig punt in de cirkel, dat dan het middelpunt is van de koorde (3). De paradox is dat elk van de drie methoden een andere uitkomst geeft. Alleen de middelste geeft een homogene verdeling.
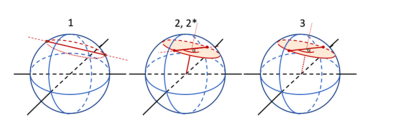
Vertaling van cirkel naar bol; van 2D naar 3D.
Schuiven met groeiende bolletjes

Pepijn Pinkse en zijn collega’s wilden ook weten hoe je van de gaten tússen de koorden de maat neemt. En om het nog complexer te maken: in drie dimensies. Zij bedachten een manier om ontelbaar kleine bolletjes te plaatsen en langzaam op te blazen. De bolletjes worden steeds een stukje verplaatst om verder groeien mogelijk te maken, zonder dat ze gesneden worden door een koorde. Zodra ze niet meer verder kunnen groeien, is de grootte van gat ter plekke bepaald. Zo is precies na te gaan hoe de grootte van de gaten verdeeld is. Deze kennis helpt de onderzoekers om de optische eigenschappen te voorspellen van de nano-mikadodoosjes die ze willen. De resultaten zijn ook interessant voor andere situaties waar rechte lijnen door ruimtelijke objecten gaan, bijvoorbeeld de meting van stralingsdoses bij Röntgenstralen, die een volume gelijkmatig moeten doorkruisen. Hier is het belangrijk om de gemiddelde lengte die de stralen afleggen, te kennen.
Het onderzoek is uitgevoerd in de groep Complex Photonic Systems, onderdeel van het MESA+ Instituut van de Universiteit Twente.
Het paper ‘Uniform line fillings’, door Evangelos Marakis, Matthias Velsink, Lars Corbijn van Willenswaard, Ravitej Uppu, en Pepijn Pinkse, verschijnt op 25 april in Physical Review E, een van de journals van de American Physical Society.





