A space-time formulation and a new discrete variational formulation for nonlinear potential flow water waves that includes wave-ship interactions
Organization:
Funded by: | 3TU-AMI |
PhD: | Sjoerd Hack |
Supervisor: | Jaap van der Vegt & Willem Vos (COPS) |
Collaboration: | Complex Photonic Systems (COPS) chair at the University of Twente |
Description:
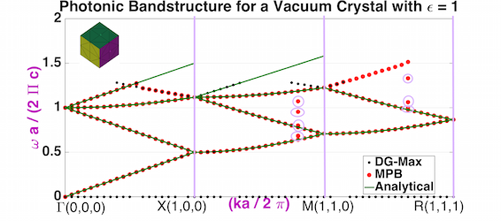
We aim to obtain a breakthrough in the understanding of photonic crystal metamaterials by means of accurate numerical methods. Such an understanding will stimulate applications in miniature LEDs, and solar energy collection.
To this end, an accurate and efficient discontinuous Galerkin finite-element eigenvalue solver for the time-harmonic Maxwell equations with periodic dielectric materials will be developed. Special attention will be given to obtain accurate solutions for non-smooth eigenfunctions near discontinuous dielectric interfaces, the modeling of finite size crystals, and the effects of manufacturing inaccuracies. These novel numerical discretizations allow the computation of optical properties of photonic band gap crystals, in particular the local density of states, and effects of unavoidable disorder.
The algorithms will be tested on GaAs photonic crystal waveguides, which have a strong dispersion, revealing slow light and enhanced light-matter interactions, and will be applied to 3D Si structures.
Publications:
Pictures:
| |