By inducing superconductivity into topological materials new types of quasiparticles can be created. It is the aim detect and manipulate these quasiparticles to test their non-abelian character, which can act as a building block for future quantum computers. To probe these effects, typical experiments are performed at low temperatures, where we probe the transport properties of a material as a function of magnetic field or temperature.
For example, we use the following material systems:
- Topological insulators (combined with magnetism)
- Topological crystalline insulators
- Higher order topological semimetals
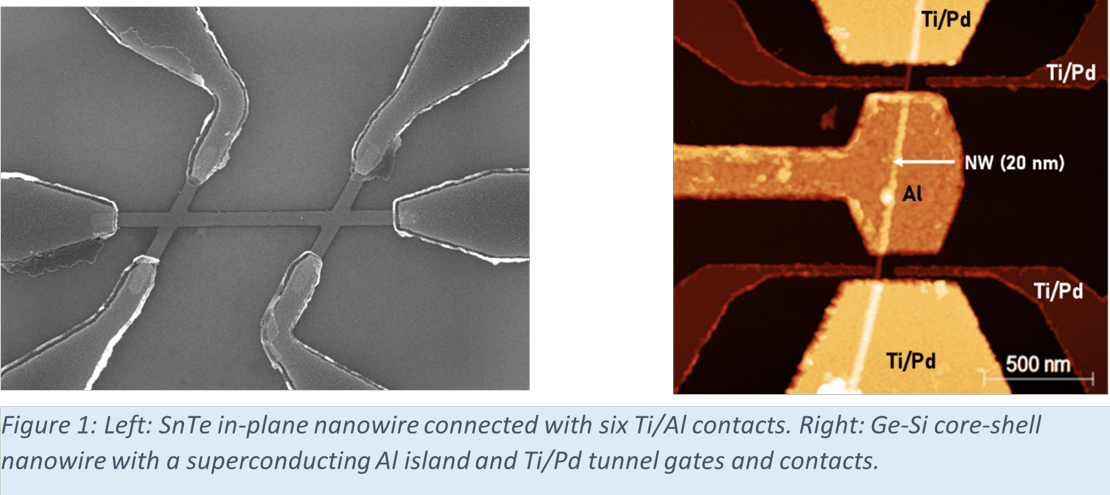
- Topological PbSnTe and Ge/Si nanowire devices
Combining semiconducting materials with a superconductor can lead to exotic physics. Theoretical predictions in 2010 [1] showed for instance that Majorana bound states can form in these hybrid super-semi devices. In our group, we want to understand the physics in these hybrid devices. Furthermore, we look for signatures of topological superconductivity. This effect can be obtained by making use of the superconducting proximity effect in a semiconducting nanowire. Topological superconductivity is a necessity to create a topological quantum computer [2].
Our group uses two types of nanowire materials to investigate signatures of topology: (i) SnTe, an intrinsic topological crystalline insulator (TCI) which should host topological surface and hinge states, and (ii) cubic Ge-Si core-shell nanowires [3] in which the topological states can be engineered by a combination of the semiconducting nanowire properties, superconducting electrodes [4,5] and an external magnetic field.
Are you interested in searching for signatures of topological superconductivity in nanowires? Do you want to know what it’s like to work in the MESA+ Cleanroom facilities? Do not hesitate to contact one of us:
M.J.G. Kamphuis MSc (Maarten)PhD Candidate[1] Lutchyn, Roman M., Jay D. Sau, and S. Das Sarma. “Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures.” Physical Review Letters 105.7 (2010): 077001.
[2] Kitaev, A. Yu. “Fault-tolerant quantum computation by anyons.” Annals of physics 303.1 (2003): 2-30.
[3] Conesa-Boj, Sonia, et al. “Boosting hole mobility in coherently strained [110]-oriented Ge–Si core–shell nanowires.” Nano letters 17.4 (2017): 2259-2264.
[4] Ridderbos, Joost, et al. “Hard superconducting gap and diffusion-induced superconductors in Ge–Si nanowires.” Nano letters 20.1 (2019): 122-130.
[5] Ridderbos, Joost, et al. “Multiple Andreev reflections and Shapiro steps in a Ge-Si nanowire Josephson junction.” Physical Review Materials 3.8 (2019): 084803.
- Higher-order topological semimetals
One of the main directions towards topological quantum computation is combining topological materials with conventional superconductivity. In our group we focus on 3D Dirac and Weyl semimetals as topological materials. These materials host topologically protected 2D surface states and 1D hinge states. Since these topological states are caused by their 3D bandstructure, these materials are called higher-order topological semimetals. We study different types of devices to understand the physics in these new materials. Especially the appearance of 1D hinge states is of interest, since inducing superconductivity into these states makes it possible to study Andreev bound states.
Our group uses different semimetals to study these higher-order states, such as Cd2As3 [1-2], BiSb [3-5] and WTe2. These materials are studied with different types of devices. The physics of the 2D surface states in these semimetals is studied with gating experiments focusing on the electronic orbits within the material. The presence of 1D hinge states in these semimetals is studied with Josephson devices and asymmetric SQUID devices to extract the current-phase relation. At last, RF measurements are used to study the Shapiro frequency response of these states.

Figure 1: Left: Asymmetric SQUID design on a Cd3As2 flake with superconducting Nb contacts. Right: Hall bar design using normal metallic Au contacts on a PtBi2 flake.
Are you interested in searching for signatures of topological superconductivity in higher-order topological materials? Do you want to know what it’s like to work in the MESA+ Cleanroom facilities? Do not hesitate to contact one of us:
[1] Zhang, C., Narayan, A., Lu, S. et al. Evolution of Weyl orbit and quantum Hall effect in Dirac semimetal Cd3As2 . Nat Commun 8, 1272 (2017).
[2] Nishihaya, S., Uchida, M., Nakazawa, Y. et al. Intrinsic coupling between spatially-separated surface Fermi-arcs in Weyl orbit quantum Hall states. Nat Commun 12, 2572 (2021).
[3] Chuan Li, Bob de Ronde, Jorrit de Boer, et al. Zeeman-Effect-Induced 0−𝜋 Transitions in Ballistic Dirac Semimetal Josephson Junctions. Phys. Rev. Lett. 123, 026802 (2019).
[4] Jorrit de Boer, Daan H. Wielens, Joris A. Voerman, et al. Nonlocal signatures of the chiral magnetic effect in the Dirac semimetal Bi0.97Sb0.03. Phys. Rev. B. 99, 085124 (2019).
[5] Chuan Li, Jorrit de Boer, Bob de Ronde, et al. 4π-periodic Andreev bound states in a Dirac semimetal. Nat. Mat. 17, 875-880 (2018).
- The quantum spin Hall effect in ultrathin hybridized topological insulators
The quantum spin Hall (QSH) effect is a prototypical phenomenon appearing in two-dimensional topological insulators (TIs) [1]. The main characteristic feature of QSH states is their spin-momentum locked edge propagation protected by time reversal symmetry, implying dissipationless transport with a single spin flavor. More specifically, if superconductivity is induced in these one-dimensional states, this could lead to the observation of helical Majorana zero modes [2].
Only recently, the QSH effect was predicted and experimentally observed in ultrathin HgTe/CdTe quantum wells, boosting experimental efforts to explore other platforms in which this exotic effect can be found [3]. In our group, we explore TIs made of bismuth-dichalcogenides, more specifically, Bi2Se3 and (BixSb1-x)2Te3 (BST). Of these two materials, it is predicted that they exhibit QSH states when they are in their ultrathin limit, that is, when their two topologically protected surfaces states hybridize and open a gap at the Dirac point [4].
Over the last years, we have gained experience in growing ultra-smooth BST thin films using molecular beam epitaxy (MBE) [5]. Furthermore, we have shown already that we can probe the hybridization effect in these films, albeit not (yet) in the QSH regime. Additionally, we have managed to contact colloidal grown Bi2Se3 nanoplatelets which show signatures of edge states around the perimeter [6]. Continuing efforts focus on further optimizing thin film growth, exploring a wider range of material thicknesses, optimizing fabrication and metal deposition techniques, and most importantly, performing transport measurements in the dilution refrigerator.
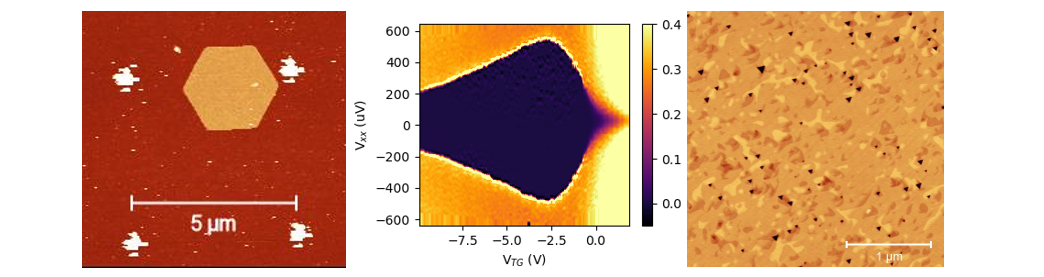
Left: AFM image of a 4 nm Bi2Se3 nanoplatelet, deposited on a Si/SiOx substrate. The white features are alignment markers that we used to align contacts to the nanoplatelet in the electron-beam lithography design.
Middle: Conductivity plot versus bias voltage and gate voltage, where a clear insulating hybridization gap is observed. This data is obtained at 80 mK in the dilution refrigerator in 6 nm thin films of BST grown with molecular beam epitaxy.
Right: AFM image of a 9 nm thin film of BST, grown with molecular beam epitaxy.
Would you like to join this ongoing project and hop on the train towards (hopefully) the QSH effect and more exotic phenomena? Do you want to explore the versatility of experimental research using many of the facilities the MESA+ Nanolab has to offer? Do not hesitate to contact me for any questions!
[1] Kane, C. L. & Mele, E. J. Z2 Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 95, 146802 (2005).
[2] Mi, S., Pikulin, D. I., Wimmer, M. & Beenakker, C. W. J. Proposal for the detection and braiding of Majorana fermions in a quantum spin Hall insulator. Phys. Rev. B 87, 241405 (2013).
[3] König, M. et al. Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 318, 766–770 (2007).
[4] Asmar, M. M., Sheehy, D. E. & Vekhter, I. Topological phases of topological-insulator thin films. Phys. Rev. B 97, 075419 (2018).
[5] Mulder, L., van de Glind, H., Brinkman, A. & Concepción, O. Enhancement of the Surface Morphology of (Bi0.4Sb0.6)2Te3 Thin Films by In Situ Thermal Annealing. Nanomaterials 13, (2023).
[6] Moes, J. R. et al. Characterization of the edge states in colloidal Bi2Se3 platelets. Nano Lett. acs.nanolett.3c04460 (2024).
