Control of cascading processes & Distributed computation of influence measures
Organization:
Funded by: | Faculty EEMCS |
PostDoc: | Wilbert Rossi |
Supervisor: | Jan Willem Polderman, Hans Zwart |
Collaboration: | Paolo Frasca UT & Grenoble, Giacomo Como (Lund university), Fabio Fagnani (Politecnico di Torino) |
Description:
Today’s world and societies rely heavily on large-scale infrastructural, biological, financial and social networks. The analysis and control of complex phenomena like congestion, epidemics, financial contagion and opinion formation cannot prescind from their network description: even if single units may be similar and fairly simple, their interactions are mediated by intricate interconnection topologies and can present non-linear and stochastic effects. Moreover, the single units need often to coordinate to achieve common, global goals.
Phenomena on complex networks are analyzed mathematically by studying a set of similar and interconnected agents. Each agent is endowed with a state and follows a simple local rule: the complexity at the global level arises from the interaction at the local level. A top-down approach to analyze features (and control processes) in large-scale networks suggests to further break the complexity and find meaningful global approximations. The sub-project Control of cascading processes use this approach to control ``domino-effects’’ in decision contexts. Instead, a bottom-up approach would exploit the interconnected units to compute global quantities using distributed schemes. This approach is used in the sub-project `Distributed computation of influence measures to compute the ability of a leader agent to influence others in an opinion formation context. Complex phenomena involving interconnected agents arise in a broad variety of context and requires diverse techniques which are developed in this project.
- Control of cascading processes
The spread of new behaviors and technologies in social and economic networks is often driven by cascading mechanisms. A simple model that captures these mechanisms is the Linear Threshold Model (LTM): the agents, interconnected in a network, choose between two actions based on a local threshold rule. The analysis of the LTM is a hard problem on general networks, which often are only known up to their statistical properties. Therefore, we use a local mean-field approach to analyze the LTM on large-scale directed networks and obtain a nonlinear, one-dimensional, recursive equation that approximates the actual fraction of adopters of a given action. We prove a concentration theorem and observe that, remarkably, the approach remains valid even if the thresholds are dynamically adjusted. These results allow the formulation of optimal control problems: future directions include the study of the structure of such control problems and the validation against the original process. - Distributed computation of influence measures
In the study of networks and dynamical processes therein, an important issue is the identification of the most influential nodes, i.e. those with the higher ability to drive the others towards a desired state. The issue depends on the process and control objective: we consider a linear opinion dynamics model where a leader node has to compete against an external opinion field. The opinions of the follower nodes converge asymptotically to values that also depend on the leader location, so, the other factor being normalized, we define the influence of the leader as the sum of the asymptotic opinions present in the social network. Inspired by an electrical analogy between asymptotic opinions and electrical potentials, we analyze a distributed message passing algorithm able to compute the influence measure. We prove that the algorithm converges asymptotically to a meaningful approximation of the nodes’ influence, on general graphs. Further directions include the extension of the proof to settings where the electrical analogy is not available
Publications:
Pictures:
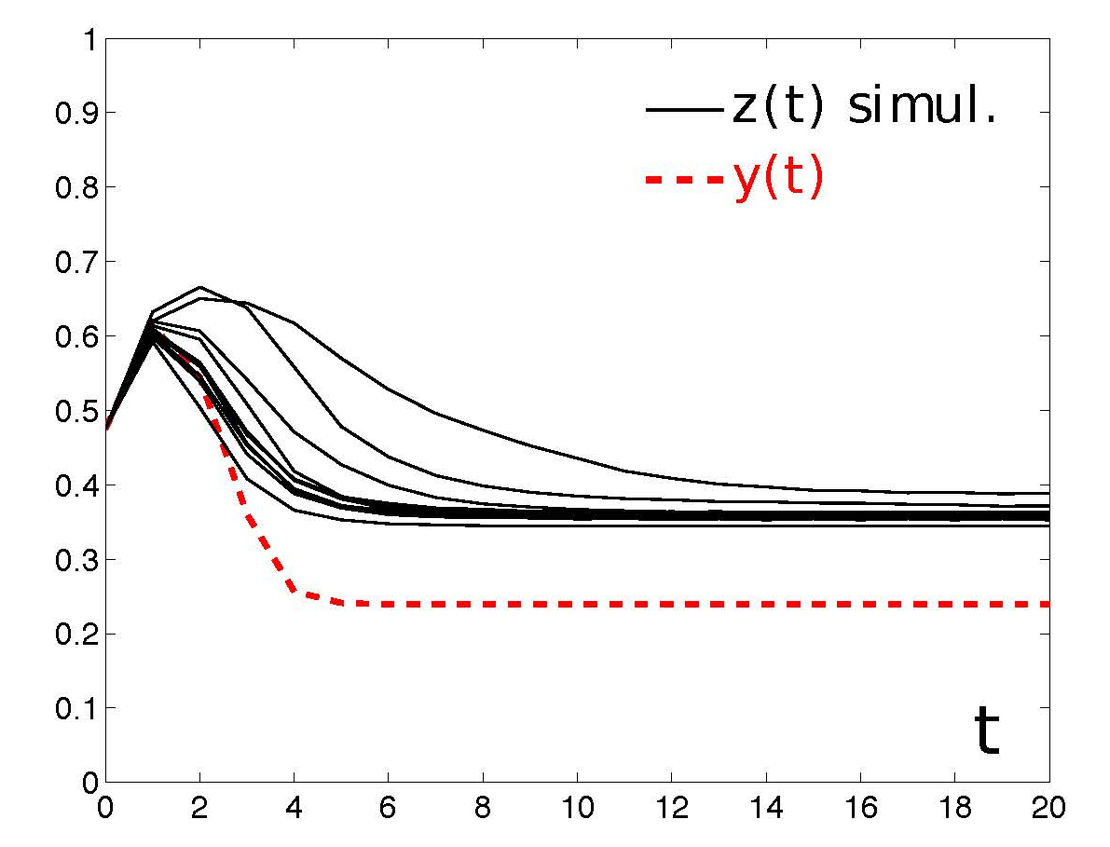
| Control of cascading processes The Linear Threshold Model has been simulated on a real topology. A few simulations of the evolution of the fraction of agents that choose the action "1" (black lines) are compared with the prediction by the local mean-field recursion (red). |
| Distributed computation of influence measures The electrical analogy between the linear opinion dynamic model with stubborn agents (left) and an electrical circuit made of resistors and voltage sources (right) |