Efficient discretization schemes for the linear Boltzmann equation
Organization:
Funded by: | UT |
PhD: | |
Supervisors: | |
Collaboration: | - |
Description:
The development and analysis of numerical approximation schemes for the linear Boltzmann equation is of primary interest in the physics and numerical analysis communities. The main obstruction for the derivation and analysis of efficient numerical methods for the Boltzmann equation are its high-dimensionality and low regularity of its solution. Novel numerical methods with reduced computational complexity and simple implementations are required to make an impact in applications.
In this project following novel approaches are addressed:
- New variational formulations for a stable and systematic discretization of the linear Boltzmann equation.
- Reduced order modeling for the linear Boltzmann equation that is based on multiscale decomposition of its solution in terms of the number of scattering events.
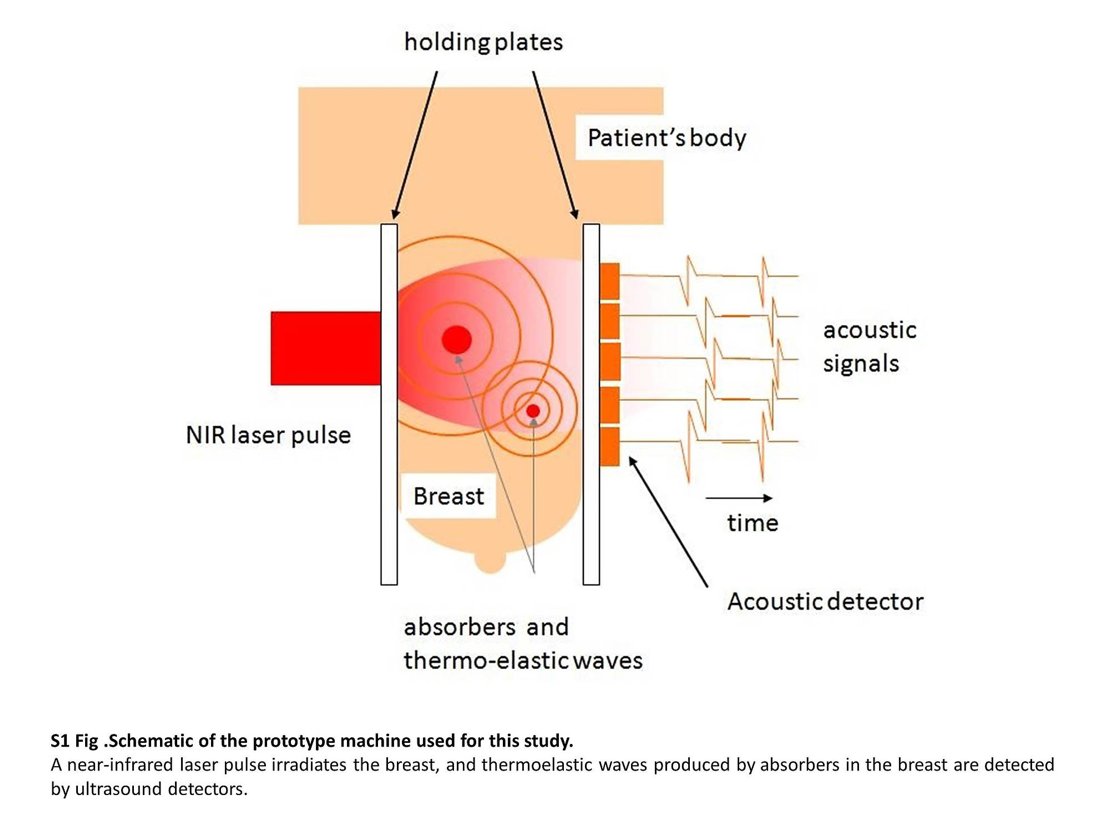
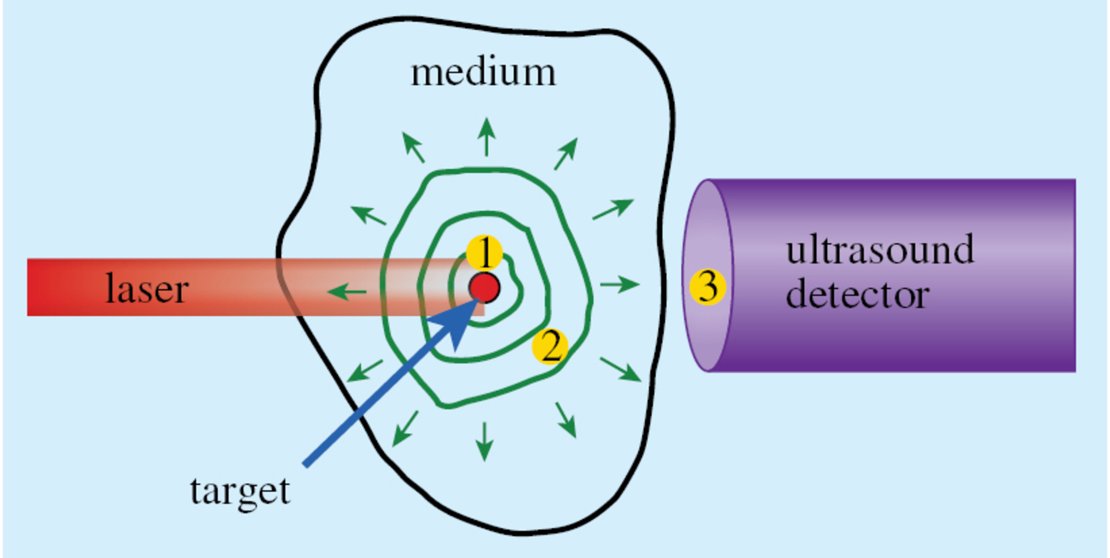
In order to test the novel methods, an important application of societal relevance is addressed, namely quantitative photoacoustic tomography, which is a non-invasive medical imaging technique that couples optical and acoustical experiments via the photoacoustic effect. Solving the linear kinetic equation fast and reliably is key in this application. With proof-of-concept implementations it is expected to make important contributions to quantitative photoacoustic tomography, thereby helping in closing the bridge to medical practice. The overall development of methods will be carried out in a flexible and modular way, so that they become accessible for larger problem classes