Organization:
Funded by: | UT/DFG |
PhD: |
|
Supervisor: | |
Daily Supervisor: | |
Collaboration: | DFG Forschungsgruppe FOR 2795 , Institute for Neurobiology, HHU Duesseldorf |
Description:
In the early 80s, Marion Diamond, a neuroscientist at UC Berkeley, studied Albert Einstein’s brain in an effort to understand what made him stand out from the rest (Diamond et al., 1985, Experimental Neurology 88, 198-204). The brain was found to have a normal functioning, normal number of neurons, synaptic connections..except in the inferior parietal lobule (part of area 39), where significantly higher number of astrocytes were reportedly found.
This is an example of how astrocytes first came to light, and the further discovery of extracellular potassium buffering and calcium signalling has led to decades of study to understand the behavior and relevance of astrocytes in the normal and pathological functioning of the brain. One of the most relevant phenomena with respect to the astrocytes is the tripartite synapse, where the star-shaped astrocyte extends its feet (called perisynaptic astrocyte processes) to a neighboring synapse, regulating synaptic transmission and supposedly releasing its own ‘gliotransmitter’. To this day, there is debate as to what exactly determines the stable functioning of the tripartite synapse and to what extent are the astrocytes repsonsible for normal/pathological synaptic transmission. 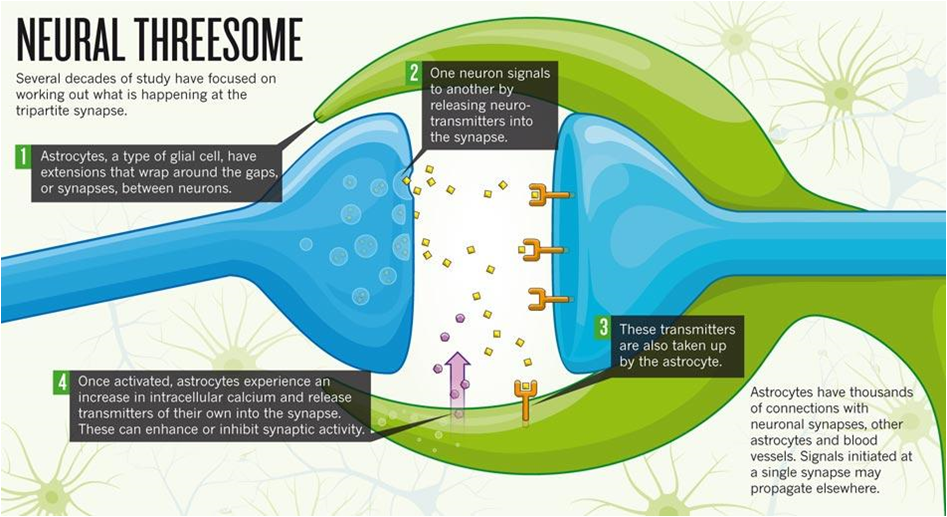
The question we ask in this project is: what are the key processes involved in the tripartite synaptic failure during low-energy conditions (metabolic failure)? To this end, we aim to answer clinically and neurobiologically relevant questions, such as the dynamics of spreading depolarizations induced by an ischemic core, and the reversal of certain ion exchangers at a single synapse during low energy conditions, from a mathematical viewpoint. A summary of some of the key processes can be seen below (taken from Bazargani et al., 2016, Nature Neuroscience 19). 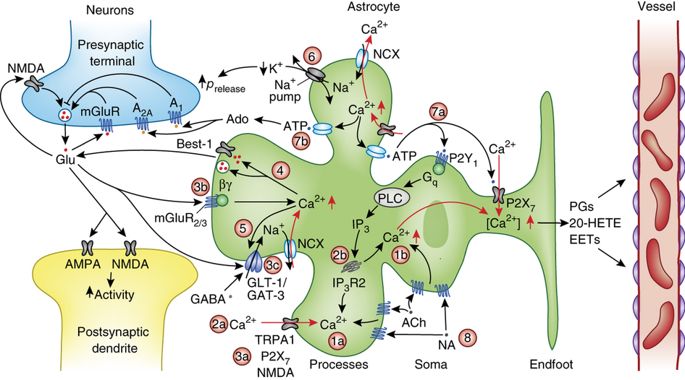
A minimal mathematical model helps us identify the most relevant processes in silico, and corroborate with the results observed from experiments. The challenges include not only introducing a minimum number of processes in the model, but also understanding the transition of dynamics across multiple scales (from single synapse to a network/field) and maintaining biophysical plausibility.
During my PhD I aim to describe biophysically realistic mathematical models of the tripartite synapse across multiple spatiotemporal scales and analyse the theoretical framework for clinically and biologically relevant dynamics.
My research interests lie in dynamical systems, bifurcation theory and spatiotemporal dynamics in neuroscience. (Cover taken from Scystyle.com, ‘Neural Threesome’ taken from Smith, 2010, Nature 468 )



